Dual-Diffusion for Binocular 3D Human Pose Estimation

NeurIPS 2024

Xiaoyue Wan, Zhuo Chen, Bingzhi Duan, Xu Zhao

{sherrywaan, chzh9311, DuanBingzhi, zhaoxu}@sjtu.edu.cn

Graphical_abstract

Abstract

Binocular 3D human pose estimation (HPE), reconstructing a 3D pose from 2D poses of two views, offers practical advantages by combining multiview geometry with the convenience of a monocular setup. However, compared to a multiview setup, the reduction in the number of cameras increases uncertainty in 3D reconstruction. To address this issue, we leverage the diffusion model, which has shown success in monocular 3D HPE by recovering 3D poses from noisy data with high uncertainty. Yet, the uncertainty distribution of initial 3D poses remains unknown. Considering that 3D errors stem from 2D errors within geometric constraints, we recognize that the uncertainties of 3D and 2D are integrated in a binocular configuration, with the initial 2D uncertainty being well-defined. Based on this insight, we propose Dual-Diffusion specifically for Binocular 3D HPE, simultaneously denoising the uncertainties in 2D and 3D, and recovering plausible and accurate results. Additionally, we introduce Z-embedding as an additional condition for denoising and implement baseline-width-related pose normalization to enhance the model flexibility for various baseline settings. This is crucial as 3D error influence factors encompass depth and baseline width. Extensive experiments validate the effectiveness of our Dual-Diffusion in 2D refinement and 3D estimation.

Overview

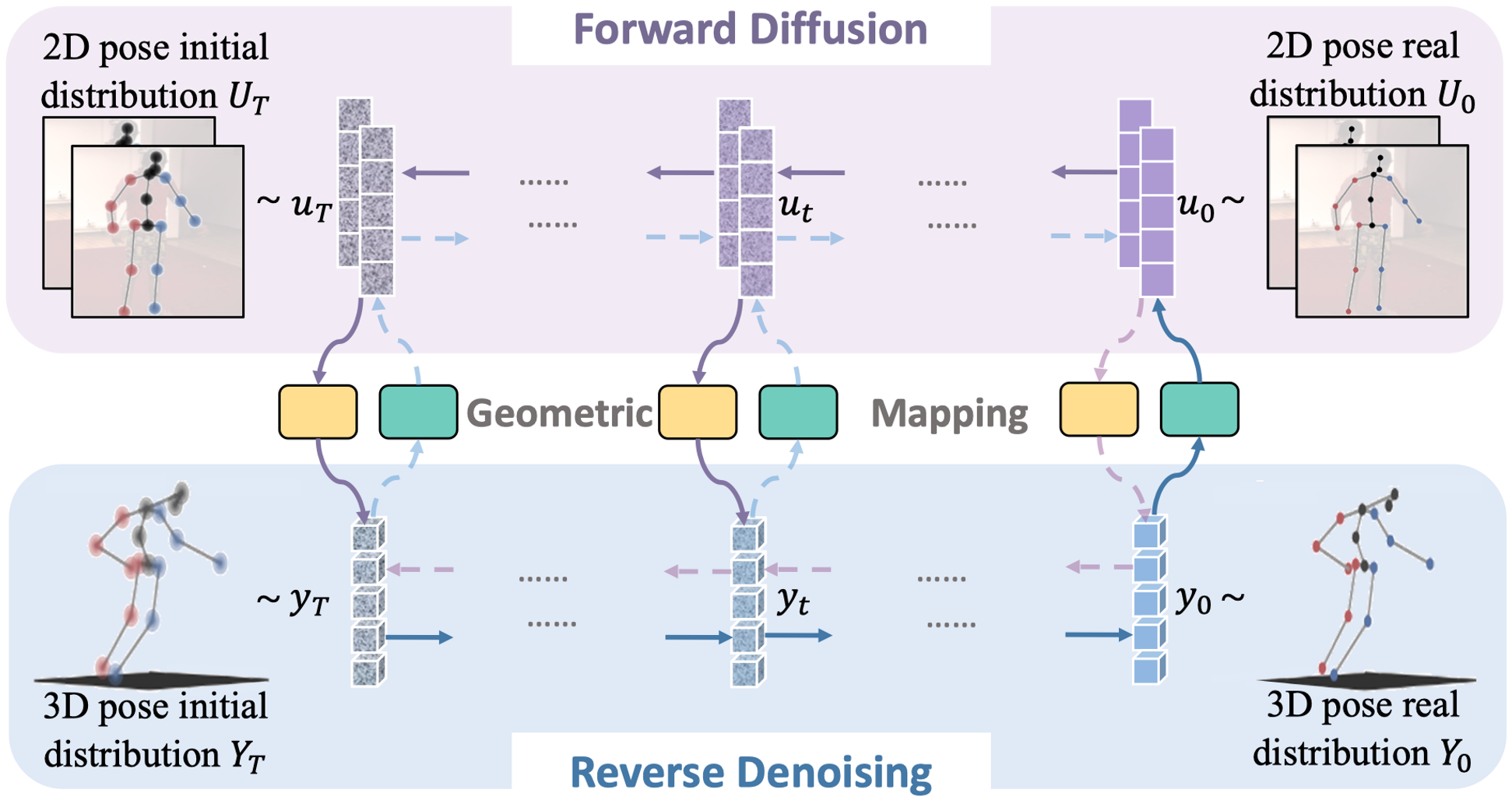
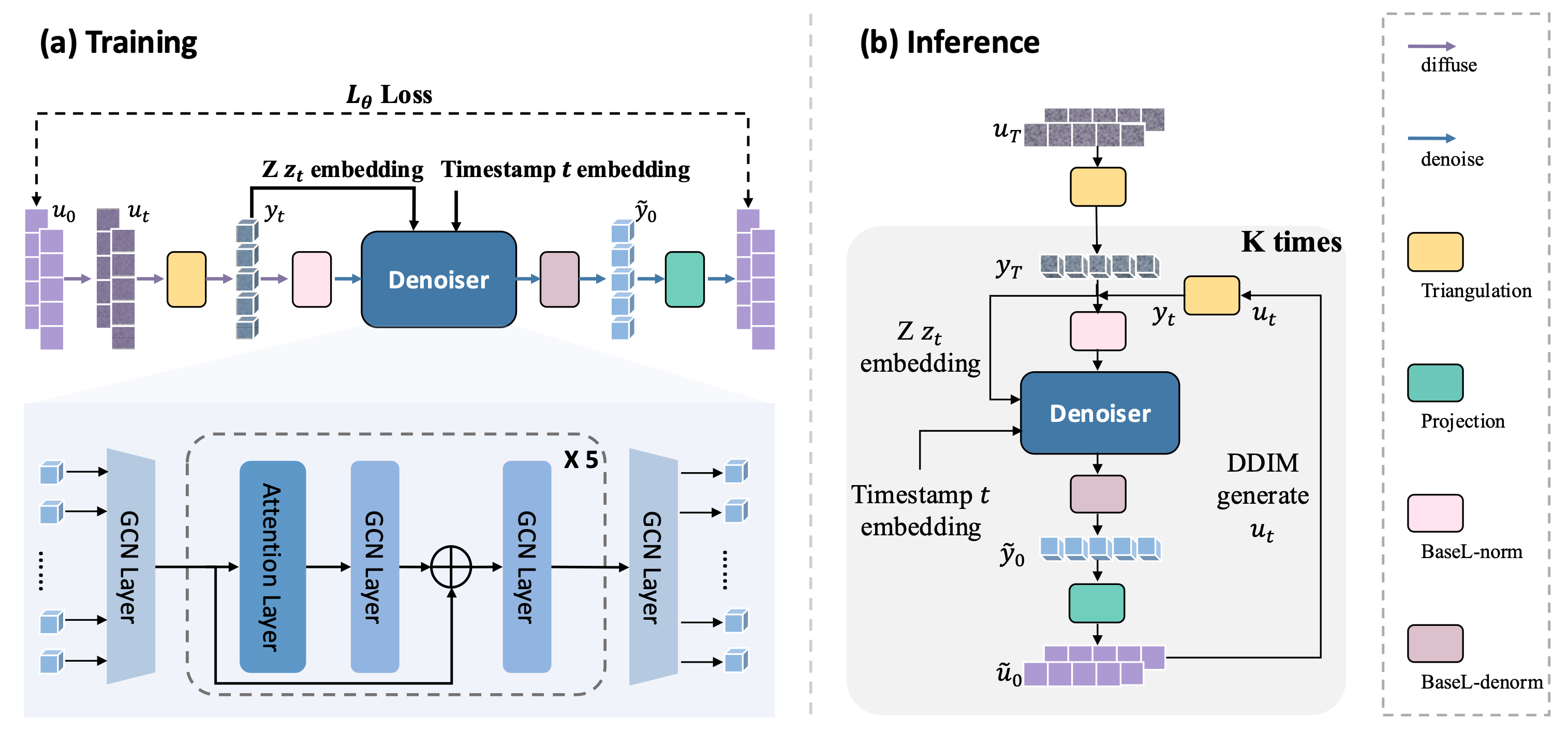
The implementation of the Dual-Diffusion model includes two steps: training and inference.

The training process is depicted as follows: 1) Initialization: Start with the ground truth 2D poses \(u_{\scriptstyle 0}\). 2) Diffusion: Randomly choose a timestamp t, add noise to generate noisy 2D poses \(u_{\scriptstyle t}\). Then Triangulation is used to reconstruct the noisy 3D poses \(y_{\scriptstyle t}\). 3) Denoising: The denoiser takes the noisy 3D poses \(y_{\scriptstyle t}\) as input and denoises them to recover original 3D poses \(\tilde{y}_0\). BaseL-norm is applied before the denoiser and BaseL-denorm is applied after. Reproject the denoised 3D poses back to 2D poses \(\tilde{u}_0\).

During the inference process, the initial binocular 2D poses \(u_{\scriptstyle T}\) estimated by a 2D detector are the input to our Dual-Diffusion model. Subsequently, the initial 3D pose \(y_{\scriptstyle T}\) is reconstructed and normalized, then fed into the denoiser to generate the plausible and accurate 3D pose \(\tilde{y}_0\), along with their corresponding binocular 2D poses \(\tilde{u}_0\). These poses \(\tilde{u}_0\) are then diffused to \(u_{\scriptstyle T}\) using the DDIM strategy for input to the next denoinsing. After iterative denoising for K times. The final 3D pose \(\tilde{y}_0\) and 2D poses \(\tilde{u}_0\) are estimated.

overview

Highlights

1) Dual-Diffusion Framework.

We propose a novel framework, Dual-Diffusion, specifically designed for binocular 3D HPE. This model simultaneously removes noise from both 2D and 3D poses by leveraging geometric mapping.

2) Uncertainty Analysis and Denoiser Enhancement.

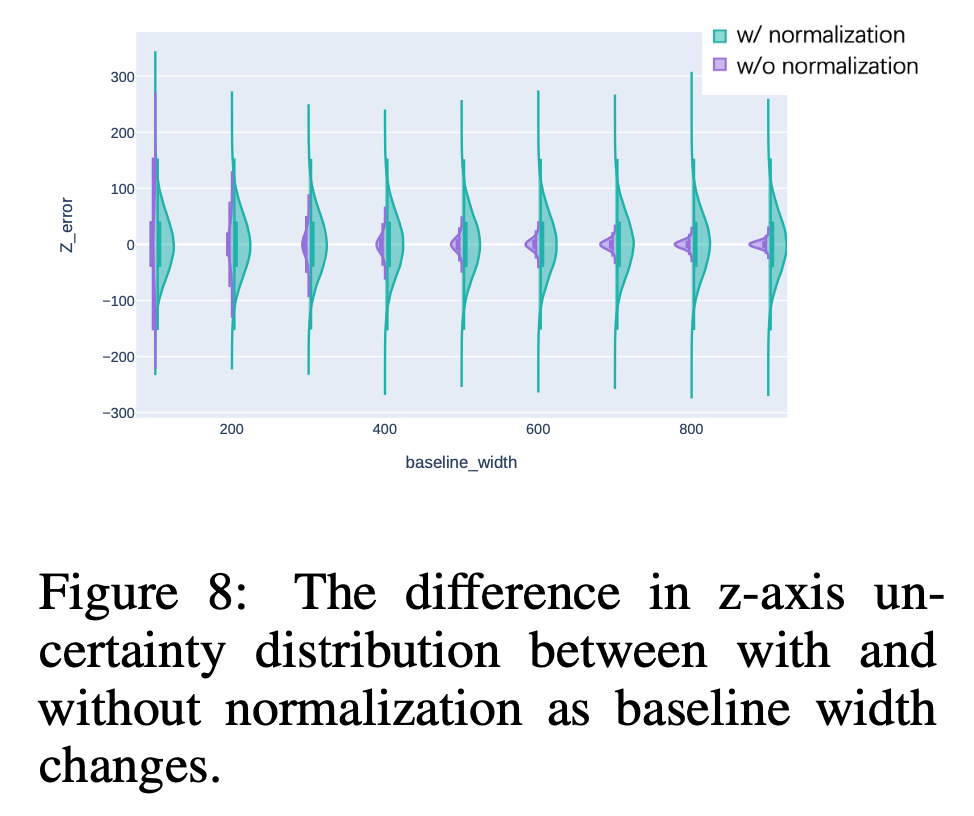
We analyze the relationship between 3D and 2D uncertainties and introduce Z-embedding and BaseL-norm to enhance the flexibility of the denoiser.

method_2_1 method_2_2

Experiments

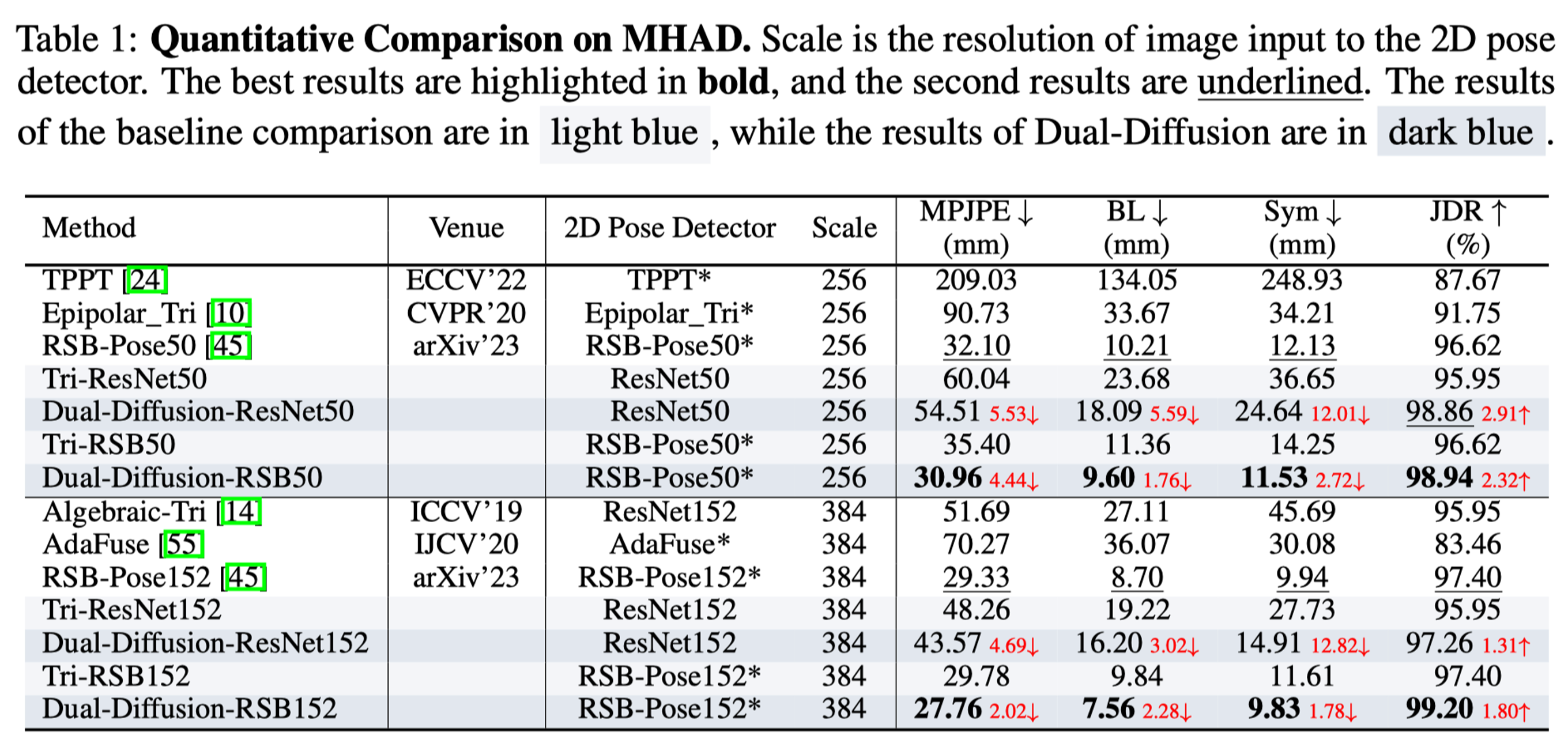
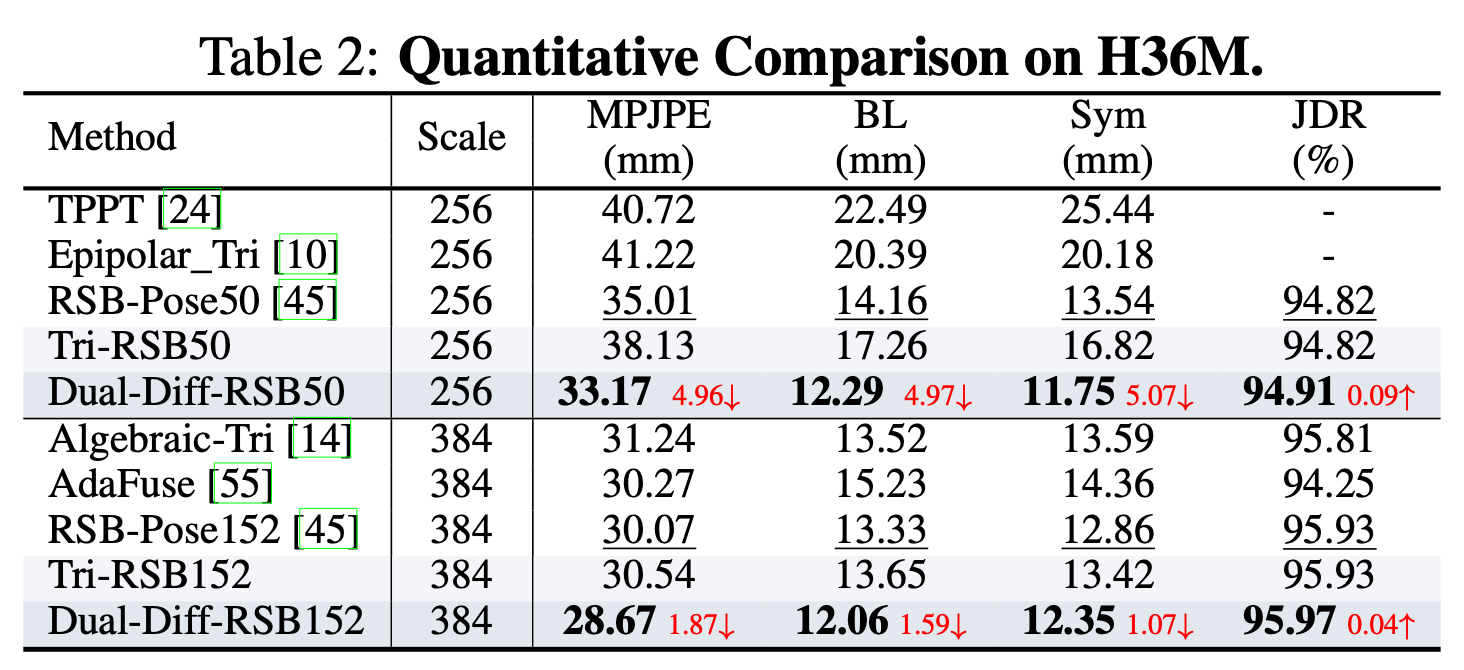
Quantitative results

The experiments are conducted on two benchmarks: 1) the short-baseline binocular benchmark, MHAD Berkeley dataset , and 2) the wide-baseline benchmark, H36M dataset.

exp_1 exp_2

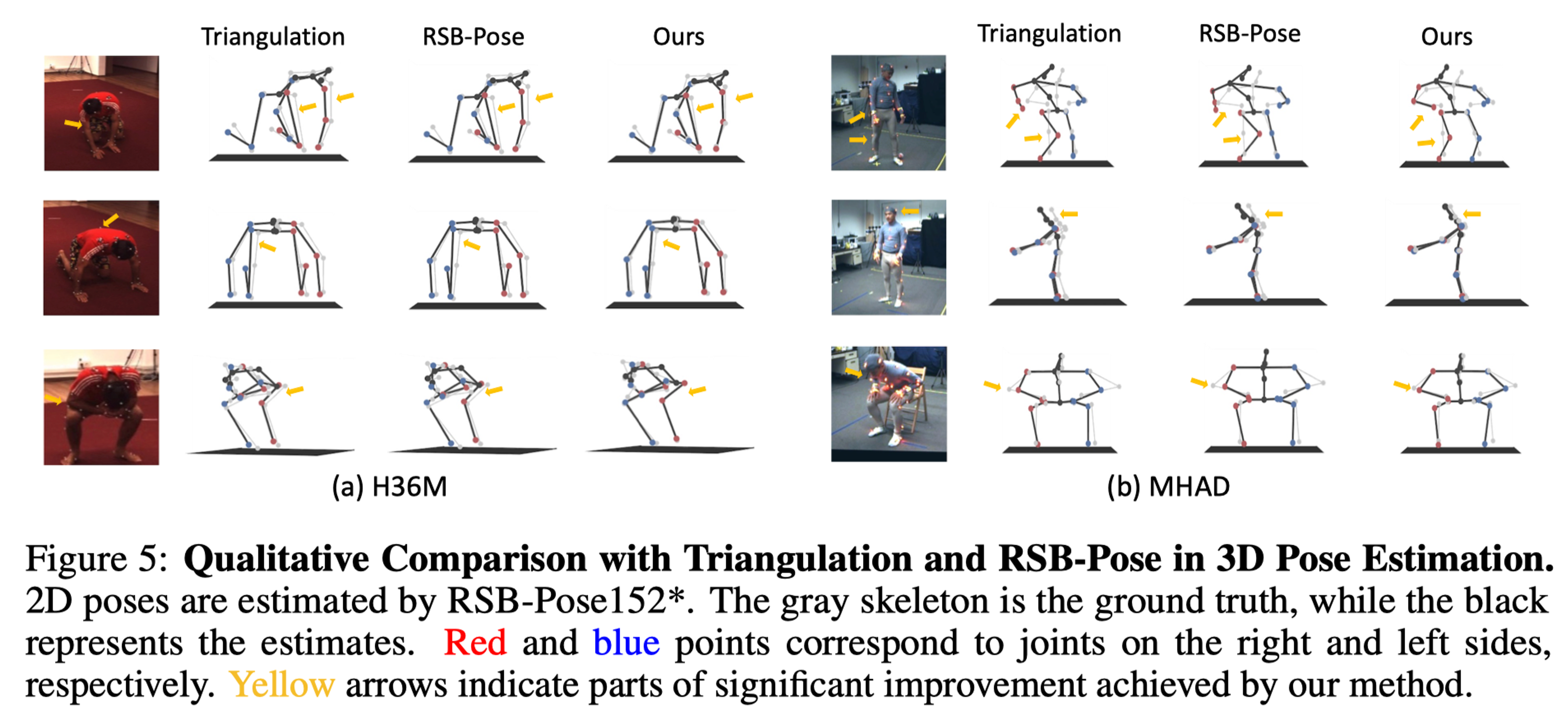
Qualitative Results

Here we provide qualitative results of Dual-Diffusion, including 2D joint diffusion and denoising comparisons as well as 3D pose estimation comparisons.

exp_1

exp_2

Citation

@inproceedings{Wan2024Dual,
    title={Dual-Diffusion for Binocular 3D Human Pose Estimation},
    author={Wan, Xiaoyue and Chen, Zhuo and Duan, Bingzhi and Zhao, Xu},
    booktitle={The Thirty-eighth Annual Conference on Neural Information Processing Systems},
    year={2024},
}